Java Program To Find Closest Value Of A Given Number In Sorted Array
We have already learned a Java Program to find the closest value of a given number in an unsorted array. In this post, we will see for a sorted array instead of an unsorted array.
In maximum array programs, logic depends on if an array is sorted or not because a logic which is optimal for an unsorted array may not be optimal for a sorted array. A logic used for a sorted array may not work with an unsorted array. For example, a binary search algorithm works on a sorted array, not on an unsorted array.
If the interviewer has not mentioned that an array is sorted or not then you must ask this question. Asking cross-questions and getting clarity on expectations or requirements is an evaluation criterion in many companies. But keep in mind – Ask valid questions. Asking more and less both are not good.
Let’s think what we understand from the above question and what needs to be asked:-
- The question says “Closest Value Of A Given Number in a sorted Array“, it means that given array is an integer array and it is sorted.
- Many may understand here that we need to look for a number which is lesser than the target number which is not expected. The closest number to target can be the target number itself or smaller than the target or greater than the target.
- Ask if an array contains negative numbers. I will show how this matters.
- You can ask if the given array contains duplicate elements.
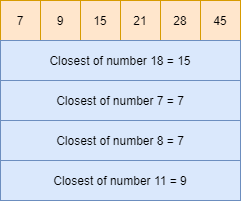
- There may be a tie. For example:- Numbers 2 & 4 both are equally closer to number 3. You can ask here which is expected. First or last. In the below examples, I have taken the first number as output.
Let’s see how negative numbers in array matters.
How many whole numbers are between 5 and 10? It is 5 numbers including 5.

How many whole numbers are between – 5 and 5? It is 10 numbers including -5.

How do we can calculate it?
By taking the difference of target and number i.e. target – number or number – target. A negative or positive difference will indicate the direction to move ( left or right). For this program, we are not worrying about the nature of difference so we will use absolute value. We can use Maths.abs() here.
10-5 = 5
5 – ( -5) = 10
So we need to calculate the actual distance from the target element properly. For example – If we have a target element as 10 then the actual distance of -5 to 10 is 10 while the actual distance of 5 to 10 is 5. It means 5 is closer to 10 than -5.
Logic to solve the above problem:-
We can use the same logic implemented for unsorted array here but since the array is sorted we can write more optimal logic. We can use a binary search algorithm here since the array is sorted. Remember this logic will not work on the unsorted array as we are using a binary search algorithm.
A binary search or half-interval search is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array.
If the target element is the same as the middle element then the target element is found.
If the target element is lesser than the middle element then we need to search in the first half of array because there is no chance of finding the target element in the second half as all elements in the second half will be greater than the target element because the array is sorted.
If the target element is greater than the middle element then we need to search in the second half because there is no chance of finding the target element in the first half as all elements in the first half will be lesser than the target element because the array is sorted. Repeat the same process till the element is found or there is the only element is left in the array.
Let’s start with some edge cases and straight logic.
Edge Cases
The length of the array should be greater than zero. Terminate the program if the length is zero.
Straight logics
- If the target element is lesser than or equal to the first element of the array then all remaining elements of the array will be greater or equal to the target element because the array is sorted. In this case, we return the first element of the array which will be closest to target.
- If the target element is greater than or equal to the last element of the array then all remaining elements of the array will be lesser or equal to the target element because the array is sorted. In this case, we return the last element of the array which will be closest to target.
Consider a sorted array below:-

If the target element is 5 which is smaller to first element i.e. 7 in the above array. We can say that all other elements i.e. 9, 15, 21, 28, and 45 are greater than 7. The first element i.e. 7 will be the only the closest element to target element 5.
If the target element is 50 which is greater than the last element i.e. 45 in the above array. We can say that all other elements i.e. 7,9,15,21 and 28 are smaller to the target element. The last element i.e. 45 will be the only the closest element to target element 50.
- Check the length of an array. If length is zero then terminate the program.
- Check if the target element is lesser than or equal to the first element of the array then return the first element of an array.
- Check if the target element is greater than or equal to the last element of the array then return the last element of an array.
- Now start implementing a binary search algorithm.
- Get the middle index which can be found using (start_index + end_index)/2. Note that the index starts from zero. An array of length 8 will have starting index as 0 and ending index as 7. We can go for positions 1 to 8 as well.
- If the target element is equal to the middle element then return the middle element.
- If the target element is lesser than the middle element then obviously our new target array will be in the first half because all elements in the second half will be farther compared to the middle element.
- If the target element is greater than the middle element then obviously our new target array will be in the second half because all elements in the first half will be farther compared to the middle element.
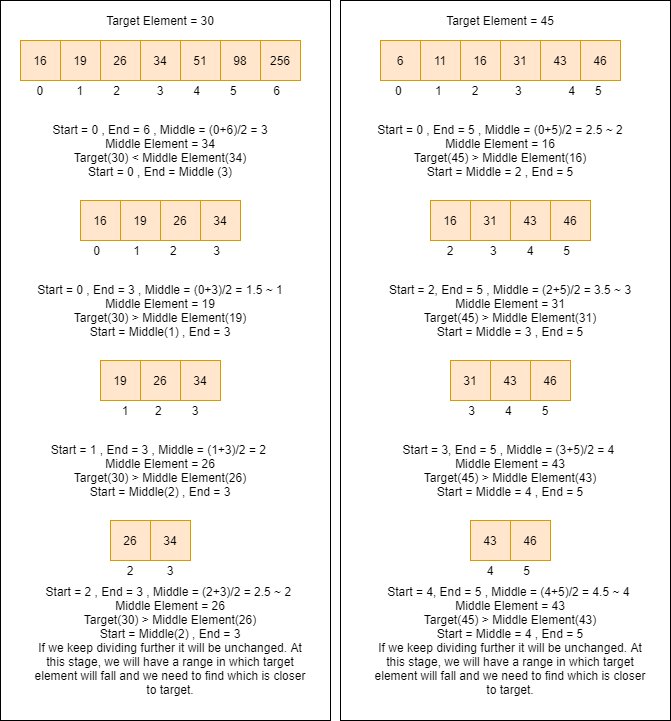
- Divide the array into halves including the middle element and repeat the process till the difference of ending index and starting index is not 1. Observe a flow diagram below step by step to understand how does binary search gives the last two sequential numbers of an array in which a number is greater than the target and another is lesser than the target.
Complete Java Program
package LeetCodeEasyPrograms;
public class FindClosestNumberOfGivenNumberInAnSortedArray {
private static int getClosetNumberOfTarget(int[] dataArray, int target) {
// Edge case - Check if array length is zero
if (dataArray.length == 0)
System.exit(1);
// Straight case - If target is smaller or equal to first element in array
if (target <= dataArray[0])
return dataArray[0];
// Straight case - If target is greater or equal to last element in array
if (target >= dataArray[dataArray.length - 1])
return dataArray[dataArray.length - 1];
// Start binary search algorithm
int start = 0;
int end = dataArray.length-1;
int mid = 0;
// Keep dividing array till further division is not possible
while (end - start != 1) {
// Calculate middle index
mid = (start + end) / 2;
// Check if middle element is equal to target
if (target == dataArray[mid])
// If yes return middle element as middle element = target
return dataArray[mid];
// Check if target is smaller to middle element. If yes, take first half of array including mid
if (target < dataArray[mid])
end = mid;
// Check if target is greater to middle element. If yes, take first half of array including mid
if (target > dataArray[mid])
start = mid;
}
// Now you will have only two numbers in array in which target number will fall
return Math.abs(target - dataArray[start]) <= Math.abs(target - dataArray[end]) ? dataArray[start]
: dataArray[end];
}
public static void main(String[] args) {
int b[] = { 1, 2, 4, 5, 6, 20, 26, 30 };
System.out.println(getClosetNumberOfTarget(b, 11));
System.out.println(getClosetNumberOfTarget(b, -5));
System.out.println(getClosetNumberOfTarget(b, 27));
System.out.println(getClosetNumberOfTarget(b, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int c[] = { 1, 2, 4, 5, 6, 20, 26 };
System.out.println(getClosetNumberOfTarget(c, 11));
System.out.println(getClosetNumberOfTarget(c, -5));
System.out.println(getClosetNumberOfTarget(c, 27));
System.out.println(getClosetNumberOfTarget(c, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int e[] = { 16, 19, 26, 34, 51, 98, 256 };
System.out.println(getClosetNumberOfTarget(e, 30));
System.out.println(getClosetNumberOfTarget(e, 31));
System.out.println(getClosetNumberOfTarget(e, 27));
System.out.println(getClosetNumberOfTarget(e, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int a[] = { -10, -6, 6, 14, 41, 58, 99 };
System.out.println(getClosetNumberOfTarget(a, -8));
System.out.println(getClosetNumberOfTarget(a, 0));
System.out.println(getClosetNumberOfTarget(a, 27));
System.out.println(getClosetNumberOfTarget(a, 10));
}
}
Output
6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 26 34 26 26 ++++++++++++++++++++++++++++++++++++++++++ -10 -6 14 6
Generally in the binary search algorithm, an array is divided excluding the middle element. But here I have included the middle element. If you want to exclude the middle element then you must need to check if the next or previous element (Depends on which half of the array you need to consider) of the middle element in the array has the sameconditional result as of middle element. If we do not check that then we may lose the closest number to target.
For example, if the array is [6,8,9,20,25,20] and the target is 11 then the middle element will be (0+5)/2 = 2.5 ~ 2 => 9.
11 > 9 -> Go to the second half of the array. If I exclude middle element i.e. 9 here which is actually closer to target 11 compared to 20, 25, and 30.
So we can ignore the middle element only if target element is greater than middle and next to a middle element or if the target element is lesser than middle and previous to the middle element
Program
package LeetCodeEasyPrograms;
public class FindClosestNumberOfGivenNumberInAnSortedArray2 {
private static int getClosetNumberOfTarget(int[] dataArray, int target) {
// Edge case - Check if array length is zero
if (dataArray.length == 0)
System.exit(1);
// Straight case - If target is smaller or equal to first element in array
if (target <= dataArray[0])
return dataArray[0];
// Straight case - If target is greater or equal to last element in array
if (target >= dataArray[dataArray.length - 1])
return dataArray[dataArray.length - 1];
// Start binary search algorithm
int start = 0;
int end = dataArray.length-1;
int mid = 0;
// Keep dividing array till further division is not possible
while (end - start != 1) {
// Calculate middle index
mid = (start + end) / 2;
// Check if middle element is equal to target
if (target == dataArray[mid])
// If yes return middle element as middle element = target
return dataArray[mid];
// Check if target is smaller to middle element. If yes, take first half of array including mid
if (target < dataArray[mid])
{
if(target < dataArray[mid-1])
end = mid-1;
else
end = mid;
}
// Check if target is greater to middle element. If yes, take first half of array including mid
if (target > dataArray[mid])
{
if(target > dataArray[mid+1])
start = mid+1;
else
start = mid;
}
}
// Now you will have only two numbers in array in which target number will fall
return Math.abs(target - dataArray[start]) <= Math.abs(target - dataArray[end]) ? dataArray[start]
: dataArray[end];
}
public static void main(String[] args) {
int b[] = { 1, 2, 4, 5, 6, 20, 26, 30 };
System.out.println(getClosetNumberOfTarget(b, 11));
System.out.println(getClosetNumberOfTarget(b, -5));
System.out.println(getClosetNumberOfTarget(b, 27));
System.out.println(getClosetNumberOfTarget(b, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int c[] = { 1, 2, 4, 5, 6, 20, 26 };
System.out.println(getClosetNumberOfTarget(c, 11));
System.out.println(getClosetNumberOfTarget(c, -5));
System.out.println(getClosetNumberOfTarget(c, 27));
System.out.println(getClosetNumberOfTarget(c, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int e[] = { 16, 19, 26, 34, 51, 98, 256 };
System.out.println(getClosetNumberOfTarget(e, 30));
System.out.println(getClosetNumberOfTarget(e, 31));
System.out.println(getClosetNumberOfTarget(e, 27));
System.out.println(getClosetNumberOfTarget(e, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int a[] = { -10, -6, 6, 14, 41, 58, 99 };
System.out.println(getClosetNumberOfTarget(a, -8));
System.out.println(getClosetNumberOfTarget(a, 0));
System.out.println(getClosetNumberOfTarget(a, 27));
System.out.println(getClosetNumberOfTarget(a, 10));
}
}
Output
6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 26 34 26 26 ++++++++++++++++++++++++++++++++++++++++++ -10 -6 14 6
If you have observed the above flow chart carefully, you must have observed that at the last we get two numbers in which target will fall. The first element is lesser than the target while the second element is greater than the target. We can put this check before dividing the array to make the logic more optimal. It may reduce number of iterations.
package LeetCodeEasyPrograms;
public class FindClosestNumberOfGivenNumberInAnSortedArray3 {
private static int getClosetNumberOfTarget(int[] dataArray, int target) {
// Edge case - Check if array length is zero
if (dataArray.length == 0)
System.exit(1);
// Straight case - If target is smaller or equal to first element in array
if (target <= dataArray[0])
return dataArray[0];
// Straight case - If target is greater or equal to last element in array
if (target >= dataArray[dataArray.length - 1])
return dataArray[dataArray.length - 1];
// Start binary search algorithm
int start = 0;
int end = dataArray.length - 1;
int mid = 0;
// Keep dividing array till further division is not possible
while (start < end) {
// Calculate middle index
mid = (start + end) / 2;
// Check if middle element is equal to target
if (target == dataArray[mid])
// If yes return middle element as middle element = target
return dataArray[mid];
// Check if target is smaller to middle element. If yes, take first half of
// array including mid
if (target < dataArray[mid]) {
// If target is greater than previous element of middle element, we have reached the deciding range
if (target > dataArray[mid - 1])
return Math.abs(target - dataArray[mid]) >= Math.abs(target - dataArray[mid - 1]) ? dataArray[mid-1]
: dataArray[mid];
end = mid - 1;
}
// Check if target is greater to middle element. If yes, take first half of
// array including mid
if (target > dataArray[mid]) {
// If target is smaller than next element of middle element, we have reached the deciding range
if (target < dataArray[mid + 1])
return Math.abs(target - dataArray[mid]) <= Math.abs(target - dataArray[mid + 1]) ? dataArray[mid]
: dataArray[mid + 1];
start = mid + 1;
}
}
// after exiting form loop, middle element will be closer
return dataArray[mid];
}
public static void main(String[] args) {
int b[] = { 1, 2, 4, 5, 6, 20, 26, 30 };
System.out.println(getClosetNumberOfTarget(b, 11));
System.out.println(getClosetNumberOfTarget(b, -5));
System.out.println(getClosetNumberOfTarget(b, 27));
System.out.println(getClosetNumberOfTarget(b, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int c[] = { 1, 2, 4, 5, 6, 20, 26 };
System.out.println(getClosetNumberOfTarget(c, 11));
System.out.println(getClosetNumberOfTarget(c, -5));
System.out.println(getClosetNumberOfTarget(c, 27));
System.out.println(getClosetNumberOfTarget(c, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int e[] = { 16, 19, 26, 34, 51, 98, 256 };
System.out.println(getClosetNumberOfTarget(e, 30));
System.out.println(getClosetNumberOfTarget(e, 31));
System.out.println(getClosetNumberOfTarget(e, 27));
System.out.println(getClosetNumberOfTarget(e, 23));
System.out.println("++++++++++++++++++++++++++++++++++++++++++");
int a[] = { -10, -6, 6, 14, 41, 58, 99 };
System.out.println(getClosetNumberOfTarget(a, -8));
System.out.println(getClosetNumberOfTarget(a, 0));
System.out.println(getClosetNumberOfTarget(a, 27));
System.out.println(getClosetNumberOfTarget(a, 10));
}
}
Output
6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 6 1 26 20 ++++++++++++++++++++++++++++++++++++++++++ 26 34 26 26 ++++++++++++++++++++++++++++++++++++++++++ -10 -6 14 6
You can clone the GIT repo from here.
If you have any doubt, feel free to comment below.
If you like my posts, please like, comment, share and subscribe.
#ThanksForReading
#HappyLearning
Find all Selenium related posts here, all API manual and automation related posts here, and find frequently asked Java Programs here.
Many other topics you can navigate through the menu.
